Let'south Toss a Coin

To illustrate the concepts behind object-oriented programming in R, nosotros are going to consider a classic take chances process (or take chances experiment) of flipping a money.

In this affiliate you volition learn how to implement code in R that simulates tossing a money one or more times.

Coin object

Think about a standard coin with 2 sides: heads and tails.

two sides of a coin

Figure one.1: two sides of a coin

To toss a coin using R, we first need an object that plays the role of a coin. How do you create such a coin? Perhaps the simplest manner to create a coin with two sides, "heads" and "tails", is with a graphic symbol vector via the combine function c():

                                                # a (virtual) money object                                coin <-                                    c("heads",                  "tails")                coin                                  #> [1] "heads" "tails"

You lot tin also create a numeric coin that shows 1 and 0 instead of "heads" and "tails":

                              num_coin <-                                    c(1,                  0)                num_coin                                  #> [one] 1 0

Likewise, you can as well create a logical coin that shows True and FALSE instead of "heads" and "tails":

                              log_coin <-                                    c(True,                  Faux)                log_coin                                  #> [1]  TRUE FALSE

Tossing a coin

Once yous have an R object that represents a coin, the next step involves learning how to simulate tossing the coin.

The of import thing to keep in mind is that tossing a coin is a random experiment: you lot either get heads or tails. One manner to simulate the activity of tossing a coin in R is with the function sample() which lets you describe random samples, with or without replacement, of the elements in the input vector.

Here's how to simulate a coin toss using sample() to take a random sample of size 1 of the elements in coin:

                                                # toss a coin                                money <-                                    c('heads',                  'tails')                                                  sample(coin,                  size =                  i)                                  #> [1] "heads"

You use the statement size = 1 to specify that y'all want to take a sample of size 1 from the input vector coin.

Random Samples

By default, sample() takes a sample of the specified size without replacement. If size = 1, it does not really matter whether the sample is done with or without replacement.

To draw two elements without replacement, use sample() like this:

                                                      # draw 2 elements without replacement                                                        sample(coin,                    size =                    2)                                      #> [1] "heads" "tails"

This is equivalent to calling sample() with the argument supervene upon = FALSE:

                                                      sample(money,                    size =                    2,                    replace =                    Imitation)                                      #> [ane] "tails" "heads"

What if y'all try to toss the money three or 4 times?

                                                      # trying to toss money three times (produces an error)                                                        sample(coin,                    size =                    three)

Notice that R produced an error bulletin:

              Error in sample.int(length(10), size, supersede, prob): cannot take a  sample larger than the population when 'supercede = FALSE'

This is considering the default behavior of sample() cannot describe more than elements than the length of the input vector.

To be able to draw more elements, you need to sample with replacement, which is washed by specifying the argument replace = Truthful, similar this:

                                                      # draw 4 elements with replacement                                                        sample(coin,                    size =                    4,                    supplant =                    Truthful)                                      #> [1] "tails" "heads" "tails" "heads"

The Random Seed

The way sample() works is past taking a random sample from the input vector. This means that every time you invoke sample() you will likely go a unlike output. For instance, when we run the following control twice, the output of the starting time phone call is different from the output in the second phone call, even though the command is exactly the same in both cases:

                                                # 5 tosses                                                  sample(coin,                  size =                  five,                  replace =                  Truthful)                                  #> [ane] "tails" "tails" "tails" "heads" "tails"                                          
                                                # another five tosses                                                  sample(coin,                  size =                  5,                  replace =                  Truthful)                                  #> [1] "heads" "heads" "heads" "heads" "tails"

In order to make the examples replicable (and then you lot can get the same output equally mine), you need to specify what is chosen a random seed. This is done with the role set.seed(). Past setting a seed, every time you apply 1 of the random generator functions, like sample(), you will get the same values.

                                                # set random seed                                                  set.seed(1257)                                                  # toss a coin with replacement                                                  sample(coin,                  size =                  4,                  supercede =                  Truthful)                                  #> [1] "tails" "heads" "heads" "tails"

Sampling with unlike probabilities

Final but not to the lowest degree, sample() comes with the argument prob which allows you to provide specific probabilities for each element in the input vector.

By default, prob = Zilch, which means that every element has the same probability of being fatigued. In the example of tossing a coin, the command sample(money) is equivalent to sample(money, prob = c(0.v, 0.5)). In the latter instance we explicitly specify a probability of 50% take a chance of heads, and fifty% chance of tails:

                                                # tossing a fair coin                                money <-                                    c("heads",                  "tails")                                                  sample(coin)                                  #> [1] "tails" "heads"                                                                  # equivalent                                                  sample(coin,                  prob =                  c(0.5,                  0.v))                                  #> [i] "tails" "heads"

Nonetheless, you can provide different probabilities for each of the elements in the input vector. For instance, to simulate a loaded coin with hazard of heads 20%, and chance of tails 80%, set prob = c(0.2, 0.eight) similar so:

                                                # tossing a loaded coin (xx% heads, 80% tails)                                                  sample(coin,                  size =                  5,                  replace =                  TRUE,                  prob =                  c(0.2,                  0.8))                                  #> [1] "heads" "tails" "tails" "tails" "tails"

Simulating tossing a coin

Now that we have all the elements to toss a coin with R, let's simulate flipping a coin 100 times, and and then use the function tabular array() to count the resulting number of "heads" and "tails":

                                                      # number of flips                                    num_flips <-                                        100                                                                          # flips simulation                                    coin <-                                        c('heads',                    'tails')                  flips <-                                        sample(coin,                    size =                    num_flips,                    replace =                    True)                                                        # number of heads and tails                                    freqs <-                                        table(flips)                  freqs                                      #> flips                                                        #> heads tails                                                                            #>    50    50

In my case, I got fifty heads and fifty tails. Your results will probably be different than mine. Sometimes you will go more "heads", sometimes you will go more "tails", and sometimes you lot will get exactly 50 "heads" and fifty "tails".

Permit's run another series of 100 flips, and find the frequency of "heads" and "tails" with the help of the table() function:

                                                      # one more 100 flips                                    flips <-                                        sample(coin,                    size =                    num_flips,                    replace =                    True)                  freqs <-                                        table(flips)                  freqs                                      #> flips                                                        #> heads tails                                                                            #>    50    50

To make things more than interesting, let'due south consider how the frequency of heads evolves over a series of n tosses (in this case northward = num_flips).

                                  heads_freq <-                                        cumsum(flips                    ==                                          'heads')                    /                                                            ane                    :num_flips

With the vector heads_freq, we can graph the (cumulative) relative frequencies with a line-plot:

                                                      plot(heads_freq,                    # vector                                                        blazon =                    'l',                    # line blazon                                                        lwd =                    2,                    # width of line                                                        col =                    'tomato',                    # color of line                                                        las =                    one,                    # orientation of tick-mark labels                                                        ylim =                    c(0,                    one),                    # range of y-axis                                                        xlab =                    "number of tosses",                    # x-axis label                                                        ylab =                    "relative frequency")                    # y-axis label                                                        abline(h =                    0.5,                    col =                    'gray50')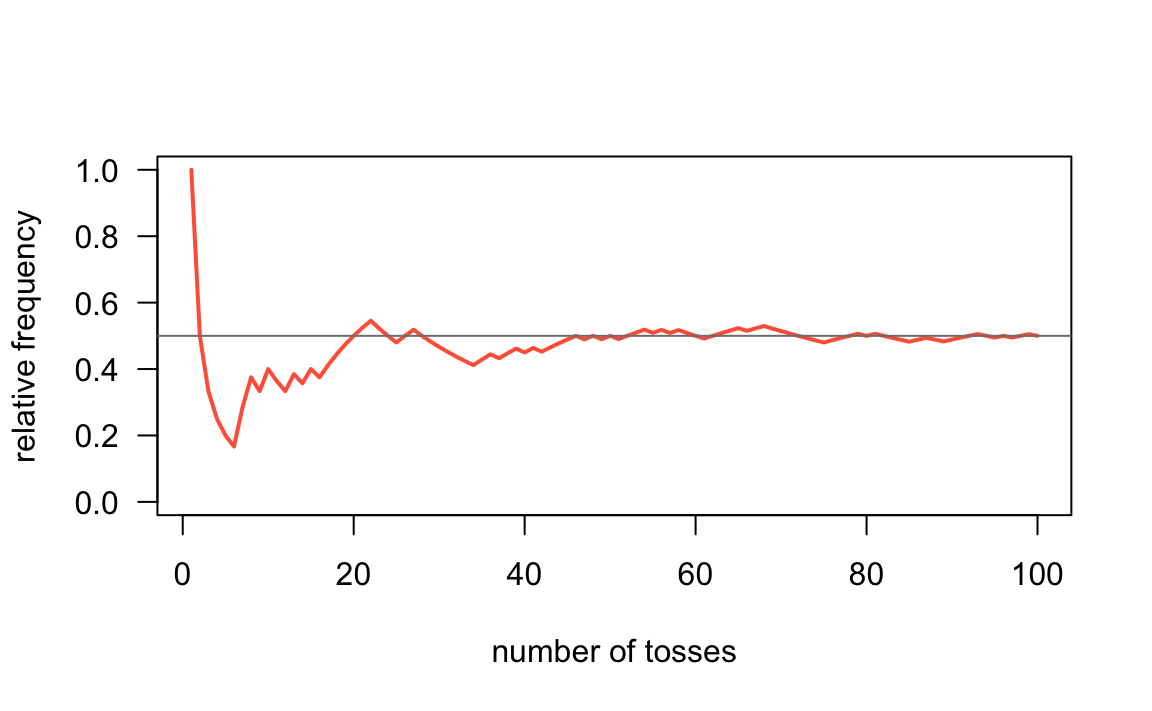

Cumulative relative frequencies of heads

Effigy one.2: Cumulative relative frequencies of heads